如何彻底删除C盘下的windows.old文件夹
本文共 292 字,大约阅读时间需要 1 分钟。
本步骤不用任何第三方工具,即可将顽固的windows.old文件夹删除,操作有风险,诸君需谨慎!!!
- windows + R 键 打开运行窗口 输入
cleanmgr,出现下面的窗口后直接点击确定即可
- 接着点击下图中的“清理系统文件”,过一会儿会出现跟下图中差不多的选项
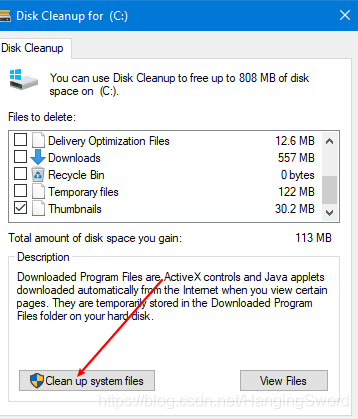 3. 在要删除的列表中找到上个版本的Windows安装,向上滑动还有一个Windows更新的日志文件,这个可以选择删除,根据自己的需求勾选想要删除的内容后点击确定即可。
3. 在要删除的列表中找到上个版本的Windows安装,向上滑动还有一个Windows更新的日志文件,这个可以选择删除,根据自己的需求勾选想要删除的内容后点击确定即可。 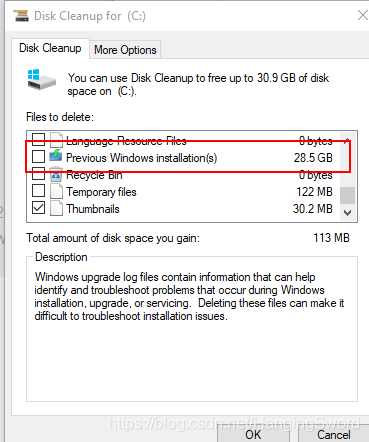 4. 等一会儿会出现一个警告,问你要不要继续,点击确定即可。
4. 等一会儿会出现一个警告,问你要不要继续,点击确定即可。
提示:将windows.old删除后,会存在无法还原到上个版本Windows的风险
转载地址:http://pmkj.baihongyu.com/
你可能感兴趣的文章